著录项信息
| 专利名称 | 基于极点配置和模糊自抗扰控制技术的四旋翼飞行器控制方法 |
| 申请号 | CN201610430502.7 | 申请日期 | 2016-06-16 |
| 法律状态 | 授权 | 申报国家 | 中国 |
| 公开/公告日 | 2016-08-31 | 公开/公告号 | CN105912009A |
| 优先权 | 暂无 | 优先权号 | 暂无 |
| 主分类号 | G05D1/08 | IPC分类号 | G05D1/08;G05D1/10查看分类表>
|
| 申请人 | 浙江工业大学 | 申请人地址 | 浙江省杭州市下城区潮王路18号浙江工业大学***
变更
专利地址、主体等相关变化,请及时变更,防止失效 |
| 权利人 | 浙江工业大学 | 当前权利人 | 浙江工业大学 |
| 发明人 | 陈强;龚相华;王音强;庄华亮;孙明轩;何熊熊 |
| 代理机构 | 杭州斯可睿专利事务所有限公司 | 代理人 | 王利强 |
摘要
一种基于极点配置和模糊自抗扰控制技术的四旋翼飞行器控制方法,建立四旋翼飞行器系统模型,初始化系统状态以及控制器参数;设计高阶的跟踪微分器;设计非线性扩张状态观测器;建立模糊规则;添加非线性反馈。设计扩张状态观测器,用于估计系统模型不确定以及外部扰动,通过极点配置法来确定扩张状态观测器参数的初值,引进模糊规则,对扩张状态观测器参数进行在线整定;设计非线性反馈控制律,保证系统跟踪误差快速稳定并收敛至零点,实现四旋翼飞行器快速稳定的位置跟踪及姿态调整。本发明解决系统模型不确定及外部扰动的问题,补偿了系统存在的模型不确定及外部扰动的影响,改善了系统性能,实现了系统快速稳定的位置跟踪及姿态调整。
1.一种基于极点配置模糊自抗扰控制技术的四旋翼飞行器控制方法,其特征在于:所述四旋翼飞行器控制方法包括以下步骤:
步骤1:建立如式(1)所示的系统运动方程:
其中,x,y,z为在地面坐标系下飞行器相对于原点的坐标,φ,θ,ψ分别代表飞行器的俯仰角,横滚角,偏航角;U1表示作用在四旋翼无人机上的合外力,p为飞行器的俯仰角角速度,为俯仰角角加速度,q为飞行器的横滚角角速度,为横滚角角加速度,r为飞行器的偏航角角速度,为偏航角角加速度,m为飞行器的质量,Ix,Iy,Iz分别为x,y,z轴上的惯性张量,τx,τy,τz分别为x,y,z轴上的力矩;
步骤2:将式(1)改写为自抗扰控制形式
其中
Δf(·)项、d(·)项分别代表模
型不确定以及外部干扰;
为了便于控制器实现,将式(2)进一步改写为
其中,
定义状态变量:z1=χ, 式(1)改写为
其中,状态变量χ存在连续的一阶导数、二阶导数,模型不确定ΔF(χ,t),外部扰动D(t)满足|ΔF(χ,t)+D(t)|步骤3:设计二阶跟踪微分器;
其中,Vd=[xd yd zd φd θd ψd]T,(·)d为期望信号, 为输入信号Vd的跟随量,为的一阶导数,r>0为速度因子;
步骤4,设计非线性扩张状态观测器,过程如下:
4.1基于扩张观测器的设计思想,定义扩张状态z3=ΔF(χ,t)+D(t),则式(4)改写为以下等效形式:
其中, N=(ΔF(χ,t)+D(t));
4.2令wi分别为式(5)中状态变量zi的观测值,i=1,2,3,定义跟踪误差 其
中 为期望信号,观测误差为eoi=zi-wi,则设计非线性扩张状态观测器表达式为:
其中,β1,β2,β3为观测器增益参数,需用极点配置法及模糊控制律确定,gj(eo1)为非线性函数滤波器,其表达式为
其中,αj=[0.1,0.3],θ=0.1;
步骤5,运用极点配置法确定观测器增益参数β1,β2,β3的初值,过程如下:
5.1令δ1=z1-w1,δ2=z2-w2,δ3=h-w3,则式(5)减去式(6)得
设h有界,且g(eo1)是光滑的,g(0)=0,g′(eo1)≠0,根据泰勒公式,式(7)写为令 则式(8)写为以下状态空间方程形式
5.2设计补偿矩阵
则式(9)写为
至此,参数βi的确定转化为li的确定,使式(10)在扰动h的作用下渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(10)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,3,使参数li满足
其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数l1,l2,l3的值,从而得到扩张状态观测器的表达式为
步骤6,引入模糊规则
以观测误差eo1,eo2为性能指标,设计模糊控制规则在线整定β1,β2,β3,其中,模糊变量分别为eo1,eo2;Δβ1、Δβ2、Δβ3代表模糊规则输出量,并在其各自论域上分别定义5个语言子集为{“负大(NB)”,“负小(NS)”“,零(ZO)”,“正小(PS)”,“正大(PB)”};选择输入量eo1,eo2的隶属度函数为高斯型(gaussmf),输出量Δβ1、Δβ2、Δβ3的隶属度函数为三角形(trimf),取eo1,eo2的基本论域分别为[-1,+1]和[-1,+1],取Δβ1、Δβ2、Δβ3的基本论域分别为[-1,1]、[-0.5,0.5]和[-0.1,0.1],模糊推理采用Mamdani型,去模糊化算法为加权平均法,表1为β1,β2,β3模糊规则表:
表1
如表1所示,建立修正参数β1,β2,β3的模糊整定规则,则得到以下参数修正表达式其中, 为极点配置得到的扩张状态观测器初始值;
步骤7,基于自抗扰控制方法设计非线性反馈动态补偿线性化控制器U,过程如下:
7.1,设计非线性反馈:
其中, δ=0.1;
7.2,根据动态补偿线性化的思想设计自抗扰控制器如下:
其中,α1=0.6,α2=0.2,运用极点配置法确定控制器参数k1,k2的取值,k1,k2为控制器参数;
7.3,运用极点配置法确定控制器增益参数k1,k2的取值:
将式(13)带入式(5)后,有
将式(14)中第二项改写为得到
其中,
令
则式(15)写为
根据泰勒公式,式(16)写为
令 则式(17)写为矩阵形式
其中,
使式(18)渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(18)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,使参数Li满足
其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数k1,k2的值。
基于极点配置和模糊自抗扰控制技术的四旋翼飞行器控制
方法
技术领域
[0001] 本发明设计一种基于极点配置和模糊自抗扰控制技术的四旋翼飞行器控制方法,适用于带有耦合非线性项,并且工作在强干扰环境下的四旋翼飞行器的位置跟踪和姿态控制。
背景技术
[0002] 四旋翼飞行器作为旋翼式无人机的一种,以其体积小、机动性能好、设计简单、制造成本低廉等优点,吸引了国内外大学、研究机构、公司的广泛关注。四旋翼飞行器非常适合用于监视、侦察等民用和军用领域。在民用领域,四旋冀飞行器主要被应用于抗灾救险、地面监测、高空航拍等;由于其隐蔽性髙,可靠性好,也被用于战场监控、军事侦察等军用领域。因此四旋翼飞行器具有广阔的市场需求和商业价值。因此,加强对无人机领域的研究,提高无人机的控制性能及控制精度已经成为一个十分重要的课题。但研究表明,四旋翼飞行器控制系统是一种多变量、强耦合的非线性控制系统,并且存在气动特性复杂,控制力矩耦合明显,飞行器参数不确定性和外部干扰敏感等问题,四旋翼飞行器控制系统的精度很难得到提高,性能也难以得到提升。因此,如何解决系统模型复杂,多个控制量之间的耦合关系,对系统外部干扰敏感等问题,改善四旋翼飞行器系统的控制性能,已经成为一个亟待解决的问题。
发明内容
[0003] 为了克服现有四旋翼飞行器控制系统部分状态及扰动不可测,以及扩张状态观测器参数难以整定等问题,本发明提出一种基于极点配置和模糊自抗扰控制技术的四旋翼飞行器控制方法,通过跟踪微分器来得到输入信号的高阶微分,采用扩张状态观测器(Extended State Observer,ESO)估计系统状态及外部扰动等不可测项并对其进行补偿,同时引入模糊规则,对扩张状态观测器参数进行在线整定,最后采用非线性反馈得出控制量,实现四旋翼飞行器快速稳定的位置跟踪及姿态调整。
[0004] 为了解决上述技术问题提出的技术方案如下:
[0005] 一种基于极点配置模糊自抗扰控制技术的四旋翼飞行器控制方法,包括以下步骤:
[0006] 步骤1:建立如式(1)所示的系统运动方程:
[0007]
[0008] 其中,x,y,z为在地面坐标系下飞行器相对于原点的坐标,φ,θ,ψ分别代表飞行器的俯仰角,横滚角,偏航角;U1表示作用在四旋翼无人机上的合外力,p为飞行器的俯仰角角速度,为俯仰角角加速度,q为飞行器的横滚角角速度,为横滚角角加速度,r为飞行器的偏航角角速度,为偏航角角加速度,m为飞行器的质量,Ix,Iy,Iz分别为x,y,z轴上的惯性张量,τx,τy,τz分别为x,y,z轴上的力矩;
[0009] 步骤2:将式(1)改写为自抗扰控制形式
[0010]
[0011] 其中
Δf(·)项、d(·)项分别代表模
型不确定以及外部干扰;
[0012] 为了便于控制器实现,将式(2)进一步改写为
[0013]
[0014] 其中,
[0015] 定义状态变量:z1=χ, 式(1)改写为
[0016]
[0017] 其中,状态变量χ存在连续的一阶导数、二阶导数,模型不确定ΔF(χ,t),外部扰动D(t)满足|ΔF(χ,t)+D(t)|<h,h为某一常值;
[0018] 步骤3:设计二阶跟踪微分器;
[0019]
[0020] 其中,Vd=[χd yd zd φd θd ψd]T,(·)d为期望信号, 为输入信号Vd的跟随量,为 的一阶导数,r>0为速度因子;
[0021] 步骤4,设计非线性扩张状态观测器,过程如下:
[0022] 4.1基于扩张观测器的设计思想,定义扩张状态z3=ΔF(χ,t)+D(t),则式(4)改写为以下等效形式:
[0023]
[0024] 其中, N=(ΔF(χ,t)+D(t));
[0025] 4.2令wi,i=1,2,3分别为式(5)中状态变量zi的观测值,定义跟踪误差
其中 为期望信号,观测误差为eoi=zi-wi,则设计非线性扩张状态观测器表
达式为:
[0026]
[0027] 其中,β1,β2,β3为观测器增益参数,需用极点配置法及模糊控制律确定,gj(eo1)为非线性函数滤波器,其表达式为
[0028]
[0029] 其中,αj=[0.1,0.3],θ=0.1;
[0030] 步骤5,运用极点配置法确定观测器增益参数β1,β2,β3的初值,过程如下:
[0031] 5.1令δ1=z1-w1,δ2=z2-w2,δ3=h-w3,则式(5)减去式(6)得
[0032]
[0033] 设h有界,且g(eo1)是光滑的,g(0)=0,g′(eo1)≠0,根据泰勒公式,式(7)写为[0034]
[0035] 令 则式(8)写为以下状态空间方程形式
[0036]
[0037] 5.2设计补偿矩阵
[0038]
[0039] 则式(9)写为
[0040]
[0041] 至此,参数βi的确定转化为li的确定,使式(10)在扰动h的作用下渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(10)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,3,使参数li满足
[0042]
[0043] 其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数l1,l2,l3的值,从而得到扩张状态观测器的表达式为
[0044]
[0045] 步骤6,引入模糊规则
[0046] 以观测误差eo1,eo2为性能指标,设计模糊控制规则在线整定β1,β2,β3,其中,模糊变量分别为eo1,eo2;Δβ1、Δβ2、Δβ3代表模糊规则输出量,并在其各自论域上分别定义5个语言子集为{“负大(NB)”,“负小(NS)”,“零(ZO)”,“正小(PS)”,“正大(PB)”};选择输入量eo1,eo2的隶属度函数为高斯型(gaussmf),输出量Δβ1、Δβ2、Δβ3的隶属度函数为三角形(trimf),取eo1,eo2的基本论域分别为[-1,+1]和[-1,+1],取Δβ1、Δβ2、Δβ3的基本论域分别为[-1,1]、[-0.5,0.5]和[-0.1,0.1],模糊推理采用Mamdani型,去模糊化算法为加权平均法,表1为β1,β2,β3模糊规则表:
[0047]
[0048] 表1
[0049] 如表1所示,建立修正参数β1,β2,β3的模糊整定规则,则得到以下参数修正表达式[0050]
[0051] 其中, 为极点配置得到的扩张状态观测器初始值;
[0052] 步骤7,基于自抗扰控制方法设计非线性反馈动态补偿线性化控制器U;,过程如下:
[0053] 7.1,设计非线性反馈:
[0054]
[0055] 其中, δ=0.1;
[0056] 7.2,根据动态补偿线性化的思想设计自抗扰控制器如下:
[0057]
[0058] 其中,α1=0.6,α1=0.2,运用极点配置法确定观测器增益参数k1,k2的取值,k1,k2为控制器参数;
[0059] 7.3,运用极点配置法确定控制器增益参数k1,k2的取值:
[0060] 将式(13)带入式(5)后,有
[0061]
[0062] 将式(14)中第二项改写为得到
[0063] 其中,
[0064] 令
[0065]
[0066] 则式(15)写为
[0067]
[0068] 根据泰勒公式,式(16)写为
[0069]
[0070] 令 则式(17)写为矩阵形式
[0071]
[0072] 其中,
[0073] 使式(18)渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(18)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,使参数Li满足
[0074]
[0075] 其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数k1,k2的值。
[0076] 本发明的技术构思为:自抗扰控制是对经典PID控制的继承与发展。通过在原有的PID框架中引入“过渡过程或者跟踪微分器”、“设计扩张状态观测器”以及“非线性反馈控制律”,使系统能够实时跟踪外界扰动以及系统不确定项,并通过反馈控制率对外界扰动及不确定项进行补偿,提高了系统的控制效率,使系统具有良好的跟踪效果。因此,自抗扰控制技术非常适合带有多变量耦合,对外部扰动敏感的四旋翼飞行器系统。
[0077] 但目前为止,扩张状态观测器的参数主要基于工程经验来进行选择。极点配置法(Pole Assignment)是通过比例环节的反馈把线性定常系统的极点移到预定位置的一种综合原理,其实质是用比例反馈去改变原系统的自由运动模式,以满足设计的要求。因此,可以通过极点配置法来确定扩张状态观测器参数的初值。
[0078] 由于四旋翼飞行器通常工作在强干扰环境下,为了实现在不同扰动情况下观测器都具有最佳的估计效果,在极点配置的基础上引进模糊规则,利用规则的自适应推理以及在一定范围内能对参数进行最佳估计的能力,达到在线整定扩张状态观测器参数的目的。
针对模型不确定以及对外部扰动敏感的四旋翼飞行器,设计了一种基于极点配置的模糊自抗扰技术的控制方法,尽可能地消除外部扰动对系统控制的影响。通过建立新的扩张状态,设计扩张状态观测器估计控制通道耦合量及外部干扰,采用极点配置法确定扩张状态观测器参数的初值,同时引进模糊规则,针对扰动情况下扩张状态观测器参数进行在线整定,最后采用非线性反馈得出控制量,实现四旋翼飞行器快速稳定的位置跟踪及姿态调整。
[0079] 本发明的有益效果为:通过运用扩张状态观测器,能对四旋翼飞行器系统状态及外部扰动进行有效观测,采用极点配置法确定扩张状态观测器参数的初值,通过引入模糊规则,在线优化扩张状态观测器参数,提高了状态估计值的可靠性,采用的非线性控制律提高了系统的控制效率,实现了对四旋翼飞行器精确的位置跟踪及姿态调整。
附图说明:
[0080] 图1为位置跟踪响应曲线,其中,(a)为在x方向上的位置跟踪响应曲线,(b)为在y方向上的位置跟踪响应曲线,(c)为在z方向上的位置跟踪响应曲线;
[0081] 图2为姿态调整响应曲线,其中,(a)为俯仰角φ的调整响应曲线,(b)为横滚角θ的调整响应曲线,(c)为偏航角ψ的调整响应曲线;
[0082] 图3为位置控制量响应曲线,其中,(a)为在x方向上的位置控制量响应曲线,(b)为在y方向上的位置控制量响应曲线,(c)为在z方向上的位置控制量响应曲线;
[0083] 图4为姿态控制力矩响应曲线,其中,(a)为俯仰角φ的控制力矩响应曲线,(b)为横滚角θ的控制力矩响应曲线,(c)为偏航角ψ的控制力矩响应曲线;
[0084] 图5为位置观测误差的响应曲线,其中,(a)为x方向上的观测误差响应曲线,(b)为y方向上的观测误差响应曲线,(c)为z方向上的观测误差响应曲线;
[0085] 图6为姿态观测误差的响应曲线,其中,(a)为俯仰角φ的观测误差响应曲线,(b)为横滚角θ的观测误差响应曲线,(c)为偏航角ψ的观测误差响应曲线;
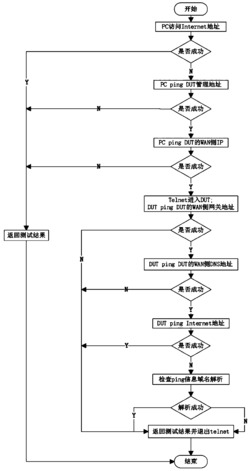
[0086] 图7为本发明的算法的基本流程。
具体实施方式:
[0087] 下面结合附图对本发明做进一步说明。
[0088] 参照图1-图7,一种基于极点配置模糊自抗扰控制技术的四旋翼飞行器控制方法,包括以下步骤:
[0089] 步骤1:建立如式(1)所示的系统运动方程:
[0090]
[0091] 其中,x,y,z为在地面坐标系下飞行器相对于原点的坐标,φ,θ,ψ分别代表飞行器的俯仰角,横滚角,偏航角;U1表示作用在四旋翼无人机上的合外力,p为飞行器的俯仰角角速度,为俯仰角角加速度,q为飞行器的横滚角角速度,为横滚角角加速度,r为飞行器的偏航角角速度,为偏航角角加速度,m为飞行器的质量,Ix,Iy,Iz分别为x,y,z轴上的惯性张量,τx,τy,τz分别为x,y,z轴上的力矩;
[0092] 步骤2:将式(1)改写为自抗扰控制形式
[0093]
[0094] 其中
Δf(·)项、d(·)项分别代表模
型不确定以及外部干扰;
[0095] 为了便于控制器实现,将式(2)进一步改写为
[0096]
[0097] 其中,
[0098] 定义状态变量:z1=χ, 式(1)改写为
[0099]
[0100] 其中,状态变量χ存在连续的一阶导数、二阶导数,模型不确定ΔF(χ,t),外部扰动D(t)满足|ΔF(χ,t)+D(t)|<h,h为某一常值;
[0101] 步骤3:设计二阶跟踪微分器;
[0102]
[0103] 其中,Vd=[χd yd zd φd θd ψd]T,(·)d为期望信号, 为输入信号Vd的跟随量,为 的一阶导数,r>0为速度因子;
[0104] 步骤4,设计非线性扩张状态观测器,过程如下:
[0105] 4.1基于扩张观测器的设计思想,定义扩张状态z3=ΔF(χ,t)+D(t),则式(4)改写为以下等效形式:
[0106]
[0107] 其中, N=(ΔF(χ,t)+D(t));
[0108] 4.2令wi,i=1,2,3分别为式(5)中状态变量zi的观测值,定义跟踪误差
其中 为期望信号,观测误差为eoi=zi-wi,则设计非线性扩张状态观测器表
达式为:
[0109]
[0110] 其中,β1,β2,β3为观测器增益参数,需用极点配置法及模糊控制律确定,gj(eo1)为非线性函数滤波器,其表达式为
[0111]
[0112] 其中,αj=[0.1,0.3],θ=0.1;
[0113] 步骤5,运用极点配置法确定观测器增益参数β1,β2,β3的初值,过程如下:
[0114] 5.1令δ1=z1-w1,δ2=z2-w2,δ3=h-w3,则式(5)减去式(6)得
[0115]
[0116] 设h有界,且g(eo1)是光滑的,g(0)=0,g′(eo1)≠0,根据泰勒公式,式(7)写为[0117]
[0118] 令 则式(8)写为以下状态空间方程形式
[0119]
[0120] 5.2设计补偿矩阵
[0121]
[0122] 则式(9)写为
[0123]
[0124] 至此,参数βi的确定转化为li的确定,使式(10)在扰动h的作用下渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(10)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,3,使参数li满足
[0125]
[0126] 其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数l1,l2,l3的值,从而得到扩张状态观测器的表达式为
[0127]
[0128] 步骤6,引入模糊规则
[0129] 以观测误差eo1,eo2为性能指标,设计模糊控制规则在线整定β1,β2,β3,其中,模糊变量分别为eo1,eo2;Δβ1、Δβ2、Δβ3代表模糊规则输出量,并在其各自论域上分别定义5个语言子集为{“负大(NB)”,“负小(NS)”,“零(ZO)”,“正小(PS)”,“正大(PB)”};选择输入量eo1,eo2的隶属度函数为高斯型(gaussmf),输出量Δβ1、Δβ2、Δβ3的隶属度函数为三角形(trimf),取eo1,eo2的基本论域分别为[-1,+1]和[-1,+1],取Δβ1、Δβ2、Δβ3的基本论域分别为[-1,1]、[-0.5,0.5]和[-0.1,0.1],模糊推理采用Mamdani型,去模糊化算法为加权平均法,表1为β1,β2,β3模糊规则表:
[0130]
[0131] 表1
[0132] 如表1所示,建立修正参数β1,β2,β3的模糊整定规则,则得到以下参数修正表达式[0133]
[0134] 其中, 为极点配置得到的扩张状态观测器初始值;
[0135] 步骤7,基于自抗扰控制方法设计非线性反馈动态补偿线性化控制器U,过程如下:
[0136] 7.1,设计非线性反馈:
[0137]
[0138] 其中, δ=0.1;
[0139] 7.2,根据动态补偿线性化的思想设计自抗扰控制器如下:
[0140]
[0141] 其中,α1=0.6,α1=0.2,运用极点配置法确定观测器增益参数k1,k2的取值,k1,k2为控制器参数;
[0142] 7.3,运用极点配置法确定控制器增益参数k1,k2的取值:
[0143] 将式(13)带入式(5)后,有
[0144]
[0145] 将式(14)中第二项改写为得到
[0146] 其中,
[0147] 令
[0148]
[0149] 则式(15)写为
[0150]
[0151] 根据泰勒公式,式(16)写为
[0152]
[0153] 令 则式(17)写为矩阵形式
[0154]
[0155] 其中,
[0156] 使式(18)渐近稳定的必要条件是补偿矩阵A的特征值全部落在复平面的左半平面上,即式(18)的极点充分的负,由此,根据极点配置法,选定期望的极点pi,i=1,2,使参数Li满足
[0157]
[0158] 其中,I为单位矩阵,令左右两边关于s的多项式的各项系数相等,则分别求出参数k1,k2的值。
[0159] 为验证所提方法的有效性和优越性,进行仿真实验,设置仿真实验中的初始条件与部分参数,即:系统方程中m=0.625,Ix=0.0023,Iy=0.0024,Iz=0.0026。控制器参数为k1=2,k2=1.25;,此外,设定扩张状态观测器中的各增益参数初值,分别取
系统各状态初始值,跟踪微分器的初始值,扩张状态观测器
状态初始值,控制器U初始值,扩张状态初始值均设为0。
[0160] 图1和图2分别给出了飞行器的位置和姿态跟踪效果。从图1和图2可以看出,飞行器在2s内跟踪上期望的位置信号,在4s内完成了对姿态的调整,并且稳态后的位置误差为
0,姿态误差始终保持在0.005的范围内,基本接近于0,表明该方法具有良好的跟踪精度。位置环和姿态环的控制器输出分别如图3和图4所示,从图3可以看出,飞行器的位置控制量均在3s内快速收敛到0,从图4(a)中可以看出飞行器的俯仰角φ控制力矩在4s内稳定在到
0.002的范围内,基本接近于0,从图4(b)中可以看出飞行器的横滚角θ控制力矩在8s内稳定在到0.002的范围内,基本接近于0,从图4(c)中可以看出飞行器的偏航角ψ控制力矩在2s内收敛稳定到0,体现了系统姿态控制的有效性。图5和图6位置和姿态的观测误差,从图5和图
6可以看出,位置观测误差均保持在0.002范围内,姿态观测误差保持在0.0006的范围内,说明扩张状态观测器具有较好的观测精度。综上所述,模糊自抗扰控制器具有较好的跟踪精度和鲁棒性。
[0161] 从仿真结果上来看,本发明的方法能有效估计和补偿系统存在的模型不确定以及外部扰动,使四旋翼飞行器能快速稳定地进行位置跟踪及姿态调整。本发明不只是限于上述实例,在本发明的基础上对其他类似的系统也可以进行有效的控制。
法律信息
- 2019-03-12
- 2016-09-28
实质审查的生效
IPC(主分类): G05D 1/08
专利申请号: 201610430502.7
申请日: 2016.06.16
- 2016-08-31
引用专利(该专利引用了哪些专利)
序号 | 公开(公告)号 | 公开(公告)日 | 申请日 | 专利名称 | 申请人 |
1
| |
2002-01-30
|
2001-06-19
| | |
2
| |
2015-03-04
|
2014-10-20
| | |
3
| |
2015-01-07
|
2014-07-22
| | |
4
| |
2015-08-26
|
2015-04-22
| | |
被引用专利(该专利被哪些专利引用)
序号 | 公开(公告)号 | 公开(公告)日 | 申请日 | 专利名称 | 申请人 | 该专利没有被任何外部专利所引用! |